关系数据库

关系

域

域是一组具有相同数据类型的值的集合。

• 如：学历：{小学，初中，高中...}
• 年龄：大于 0 小于 150 的整数

笛卡尔积

• 给定一组域 D1,D2,...Dn，这些域可以是相同的，也可完全不同，则 D1,D2,...Dn 的笛卡尔积为：

$$D_1\times D_2\times ...\times D_n=\{(d_1,d_2,...,d_n)|di\in D_i,i=1,2,...,n\}$$

• 所有域的所有取值的一个组合
• 不能重复
• 笛卡尔积的表示方法：笛卡尔积可表示为一张二维表，表中的每行对应笛卡尔积的一个袁术，表中的每列对应一个域。

例子：

域D1 = {1,2,3}，域D2 = {A,B}，求 D1 与 D2 的笛卡尔积：

D1 x D2 = {(1,A),(1,B),(2,A),(2,B),(3,A),(3,B)}

• 元组：笛卡尔积中每一个元素(d1, d2, ..., dn)叫做一个元组，如果它包括 n 个值，就叫 n 元组或简称为元组，如上述中的(1,A)，(1,B)；
• 分量：笛卡尔积元素(d1,d2,...,dn)中的每一个值 di 叫做一个分量，如例题中 1，A，B 都是分量
• 基数：若 Di(i = 1,2,...,n)为有限集，其基数为 mi(i=1,2,...,n)，则 D1 x D2 x ... x Dn 的基数 M 为：M = m1 x m2 x ... x mn，上述例子中的 D1 与 D2 的笛卡尔积的基数就是 3x2=6
• 笛卡尔积不满足交换律

关系

• 笛卡尔积 D1 x D2 x ... Dn 的子集叫做在域 D1,D2,...Dn 上的关系，表示为 R(D1,D2,...Dn)

• 这里的 R 表示关系的名字，n 是关系的目或者度

• 一般来说，D1、D2、...、Dn 的笛卡尔积是没有实际意义的，从中取出右实际意义的元组才能构成关系。

• 关系是笛卡尔积的有限子集，无限关系在数据库系统中是无意义的

• 关系是笛卡尔积的子集，所以关系也是一个二维表，表的每行对应一个元组，表的每列对应一个域。由于域可以相同。为了加以区分，必须对每列取一个名字，称为属性。

• 笛卡尔积不满足交换律，但关系满足交换律，这是因为每个列的属性名可以取消元组的有序性

• 候选码：能够唯一标识关系中一个元组的某一属性组，称为候选码

• 候选码所包含的属性可能是一个属性，也可能是多个属性，在最极端的情况下，关系的所有属性才能称为候选码，称为全码。

• 一个关系的候选码可能不只一个，如果有多个候选码，选定其中一个作为主码

• 候选码的诸属性称为主属性，不存在任何候选码中的属性称为非主属性。

关系的性质

• 关系中的每个属性是不可分解的，就是之前提到的不能表中有表，这个性质也是关系模型对关系最基本的要求。
• 表中各列取自同一个域
• 不同的列可以来自同一个域
• 列的次序可以任意交换，不改变关系的实际意义，这是因为属性名取消了关系元组的有序性
• 表中不允许出现完全相同的两行
• 行的次序无关紧要，可以任意交换，不会改变关系的意义

关系模式

型和值

• 关系模式是型
• 关系是值
• 关系模式是对关系的描述
  • 元组集合的结构：
    • 属性构成
    • 属性来自的域
    • 属性域域之间的映像关系
  • 元组语义以及完整性约束条件
  • 属性间的数据以来关系集合
• 关系模式是静态的
• 关系是动态的

关系模式

• 关系模式可以形式化地表示为：R(U, D, DOM, F)
• R 为关系名
• U 为组成该关系地属性名集合
• D 为属性组 U 中属性所来自地域
• DOM 为属性向域的映像集合
• F 为属性间数据的依赖关系集合
• 关系模式可以简化为二元组 R(U)或者 R(A1, A2, ... , An)

关系数据库

关系数据库

• 关系数据库是基于关系模型的数据库
• 在关系模型中，实体及实体间的联系都是用关系来表示。
• 在一个给定的现实世界应用领域中，所有实体及实体之间联系所形成的集合就构成了一个关系数据库
• 关系数据库的型：数据库的描述。它包含若干域的定义以及在这些域上定义的若干关系模式。
• 关系数据库的值：这些关系模式在某一时刻对应的关系集合
• 在数据库中，关系模式是型，关系是值，二者通常统称为关系数据库

关系数据操作

• 常用的关系操作：
  • 查询操作：选择、投影、连接、除、并、差、交、笛卡尔积；其中选择、投影、并、差、笛卡尔积是五种基本操作
  • 数据更新”插入、删除、修改
• 关系操作的特点：集合操作方式：操作的对象和结果都是集合，一次一集合的方式

实体完整性

• 实体完整性规则：若属性 A 是基本关系 R 的主属性，则 A 不能取空置，这里的主属性是指候选码中包含的所有属性
• 空值就是“不知道”或“不存在”或“无意义”的值

关系模型必须遵守实体完整性规则的原因：

• 实体完整性规则是针对基本关系而言的。一个基本表通常对应现实世界的一个实体集或多对多联系。
• 现实世界中的实体和实体间的联系都是可区分的，即它们具有某种唯一性标识
• 相应的，关系模型中以主码作为唯一性标识
• 主码中的属性即主属性不能取空值

参照完整性

关系的引用

• 在关系模型中实体及实体间的联系都是用关系来描述的，自然存在着关系与关系间的引用
• 商品关系中引用了供应商关系的主码“供应商编码”
• 销售关系中引用了学生关系的主码“学号”和商品关系的主码“商品编码”

外码

• 定义：设 F 是基本关系 R 的一个或一组属性，但不是关系 R 的码，K 是基本关系 S 的主码。如果 F 与 K 相对应，则称 F 是 R 的外码，并称基本关系 R 为参照关系，基本关系 S 为被参照关系或目标关系。

一些理解

• 外码必须是本关系的一个或一组属性
• 外码不是本关系的码
• 外码与另一个关系（可能是同一关系）的主码相对应

说明：

• 关系 R 和 S 不一定是不同的关系
• 目标关系 S 的主码 K 和参照关系的外码 F 必须定义在同一个（或一组）域上
• 外码并不一定要与相应的主码同名
• 当外码与相应的主码属于不同关系时，往往取相同的名字，以便于识别

参照完整性规则

参照完整性规则：若属性（或属性组）F 是基本关系 R 的外码，它与基本关系 S 的主码 K 相对应（基本关系 R 和 S）不一定是不同的关系，则对于 R 中每个元组在 F 上的取值必须为：

• 或者取空值（F 的每个属性值均为空值）
• 或者等于 S 中每个元组的主码值

用户定义的完整性

用户定义的完整性：针对某一具体应用环境，给出关系数据库的约束条件，这些约束条件就是反映某一具体应用所设计的数据必须满足的语义要求

用户定义的完整性约束主要包括：

• 唯一值约束（UNIQUE）
• 非空值约束（NOT NULL）
• 检查约束（CHECK）
• 缺省值约束（DEFAULT）

传统集合运算

假设 R 和 S 都是关系，具有相同的目 n，且相应地属性取自同一个域

• 并：是由属于 R 或属于 S 的元组组成
• 交：是由既属于 R 又属于 S 的元组组成
• 差：是由属于 R 但不属于 S 的元组组成

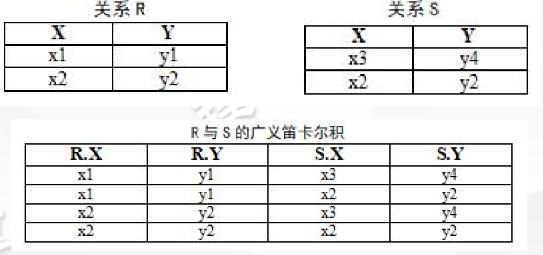
广义笛卡尔积：如果 R 和 S 都是关系，分别是 n 目和 m 目，则 R 和 S 的广义笛卡尔积是一个（n+m）列的元组的集合。元组的前 n 列是关系 R 的一个元组，后 m 列是关系 S 的一个元组。如果 R 有 k1 个元组，S 有 k2 个元组，则关系 R 和关系 S 的广义笛卡尔积有 k1xk2 个元组。

专门的关系运算

• 选择运算：行的角度
• 投影运算：从 R 中选择出若干属性列组成新的关系，列的角度，投影之后不仅取消了原关系中的某些列，而且还可能取消某些元组（避免重复行）
• 连接运算
  • theta 连接：从行的角度进行运算，连接结果的列是参加原酸的关系的列的组合
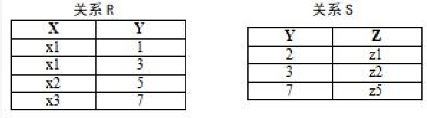
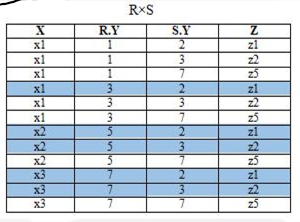
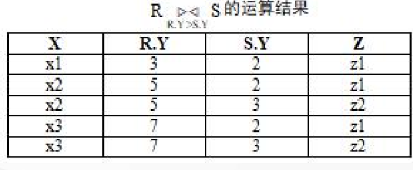
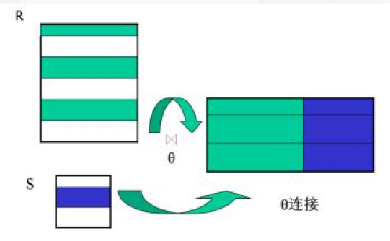
  • 等值连接：当 theta 取“=”时
  • 自然连接：特殊的等值连接，要求两个关系中进行比较运算的分量必须时相同的属性组，并且在结果中把重复的属性列去掉
• 除运算【略】