数组

数组

特点：

• 结构固定
• 每一个维度上的元素同构

数组运算：

• 给定位置，存取相应数据元素。
• 给定位置，修改数据元素的值。
• 数组一般不做添加或删除操作。

数组顺序存储：

• 以行序为主序。

$$Loc(a_{ij})=Loc(a_{00})+(i\times n+j)\times L$$

• 以列序为主序。

$$Loc(a_{ij})=Loc(a_{00})+(j\times m+i)\times L$$

特殊矩阵

对称矩阵

$$n=\{\begin{array}{ll}& \text{i}(i+1)/2+j,i>=j\\ & \text{j}(j+1)/2+i,i<j\end{array}$$

三角矩阵

$$n=\{\begin{array}{ll}& \text{i}(i+1)/2+j,i>=j\\ & \text{n}(n+1)2,i<j\end{array}$$

三对角矩阵

（按行主序为例）

• 总长度：3n-2
• 已知k(0<=k<=3n-3)
• i = (k+1)/3
• j = (k+1)%3+i-1

稀疏矩阵

定义

• 非零元个数<<零元个数
• 分布没有规律
• 对矩阵 M：
  • density = M 中非零元总数/M 的元素总数。
  • density<=5%时，则称 M 为稀疏矩阵。
  • density 称为 M 的稠密度。

压缩存储

• 三元组法
• 存储非零元的行、列下标及其值。
• 存储矩阵的行、列维数。
• 三元组：{0，1，12}，{0，2，9}，{3，1，-3}······
• 行列式维数：（6，7）
• 非零元个数：8

0	6	7	8
1	1	2	12
2	1	3	9
3	3	1	-3
4	3	6	14
5	4	3	24
6	5	2	18
7	6	1	15
8	6	4	-7

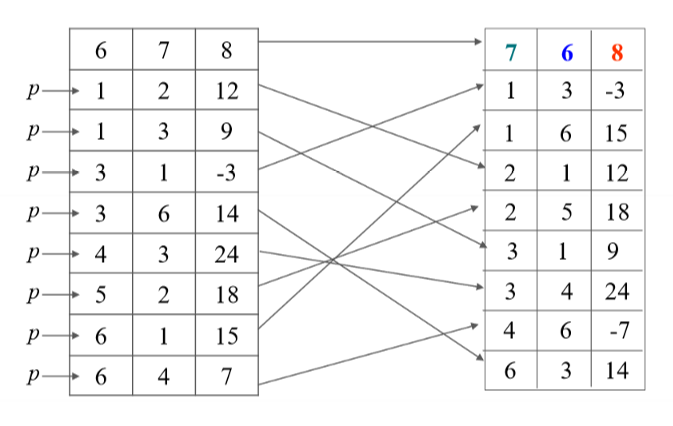
快速转置

一般的矩阵转置:

for(col = 0; col < n; col++){
    for(row = 0; row < m; row++){
        n[col][row] = m[row][col];
    }
}
//时间复杂度：T(n) = O(mxn)

快速转置：

• 按 M 中三元组次序转置，转置结果放入 N 中恰当位置。
• 确定 M 中每一列第一个非零元在 N 中位置。
  • 为确定这些位置，应先计算 M 中每一列中非零元个数。
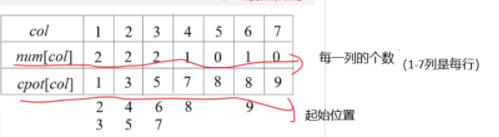
• 设两个辅助数组
  • num[col]：表示 M 中第 col 列中非零元个数。
  • cpot[col]：指示 M 中第 col 列第一个非零元在 N 中位置。
• 显然有
  • cpot[1] = 1
  • cpot[col] = cpot[col-1] + num[col-1]; (2<=col<=M[0])

准备：

#include<iostream>
#include<vector>
#include<cstring>

using namespace std;

int num[5][5] = {
    {1,1,1,1,1},
    {0,0,0,1,0},
    {0,0,1,0,0},
    {0,1,0,0,0},
    {1,1,1,1,1},
};

链式存储：

struct elements
{
    int col;
    int row;
    int val;
    elements* next;
    elements(int col, int row, int val):
    col(col),row(row),val(val),next(NULL){}
};
//这里偷点懒就不把长度传进来了 O(∩_∩),数组定义的全局变量
void num2elements(elements* head){
    elements* temp = NULL;
    for(int i = 4; i >= 0; i--){
        for(int j = 4; j >= 0; j--){
            if(num[i][j] != 0){
                temp = new elements(i, j, num[i][j]);
                temp->next = head->next;
                head->next = temp;
            }
        }
    }
}

顺式存储：

vector<vector<int>> elements;
vector<int> temp;
void num2elements(){//转换 3 元组
    temp.push_back(5);
    temp.push_back(5);
    temp.push_back(13);
    elements.push_back(temp);
    temp.clear();
    for(int i = 0; i < 5; i++){
        for(int j = 0; j < 5; j++){
            if(num[i][j] != 0){
                temp.push_back(i);
                temp.push_back(j);
                temp.push_back(num[i][j]);
                elements.push_back(temp);
                temp.clear();
            }
        }
    }
}

转置操作：

int count[5];
int cpot[5];

int result[14][3];//转置后的结果；

void trans(){
    //init count
    for(int i = 0; i < elements.size(); i++){
        count[elements[i][1]]++;
    }
    //init cpot
    int sum = 0;
    for(int i = 0; i < 5; i++){
        cpot[i] = sum;
        sum += count[i];
    }
    int index = 0;
    for(int i = 1; i < 14; i++){
        index = ++cpot[elements[i][1]];

        result[index][0] = elements[i][1];
        result[index][1] = elements[i][0];
        result[index][2] = elements[i][2];
    }
    //把行列及非零个数进行赋值
    result[0][0] = elements[0][1];
    result[0][1] = elements[0][0];
    result[0][2] = elements[0][2];
}

int T_num[5][5];
void print_result(){
    memset(T_num, 0, sizeof(T_num));
    for(int i = 1; i < 14; i++){
        T_num[result[i][0]][result[i][1]] = result[i][2];
    }
    for(int i = 0; i < 5; i++){
        for(int j = 0;j < 5; j++){
            cout << T_num[i][j] << ", ";
        }
        cout << endl;
    }
}

主函数：

int main(){
    //elements* head = new elements(5, 5, 13);
    //num2elements(head);
    num2elements();
    for(int i = 0; i < elements.size(); i++){
        for(int j = 0; j < 3; j++){
            cout << elements[i][j] << ", ";
        }
        cout << endl;
    }
    cout << "*************************" << endl;
    trans();
    for(int i = 0; i < 14; i++){
        for(int j = 0; j < 3; j++){
            cout << result[i][j] << ", ";
        }
        cout << endl;
    }
    cout << "*************************" << endl;
    print_result();
    return 0;
}

结果：

/*
5, 5, 13, 
0, 0, 1,
0, 1, 1,
0, 2, 1,
0, 3, 1,
0, 4, 1,
1, 3, 1,
2, 2, 1,
3, 1, 1,
4, 0, 1,
4, 1, 1,
4, 2, 1,
4, 3, 1,
4, 4, 1, 
*************************
5, 5, 13,
0, 0, 1,
0, 4, 1,
1, 0, 1,
1, 3, 1,
1, 4, 1,
2, 0, 1,
2, 2, 1,
2, 4, 1,
3, 0, 1,
3, 1, 1,
3, 4, 1,
4, 0, 1,
4, 4, 1,
*/

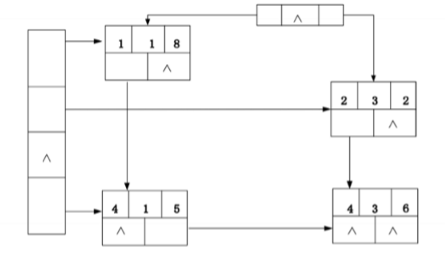
十字链表

原因：三元组表元素移动

• 对顺序存储的三元组表，移动元素的时间开销大
• 为维护行主序、列有序，可能产生更多开销

十字链表是稀疏矩阵的另一种存储策略

• 每个非零元为一个结点，每个结点含五个域。
  • 其中，行域 i、列域 j、值域 v 分别表示非零元素的行下标、列下标和值。
  • 向右域 right 链接同一行中下一个非零元素。
  • 向下域 down 链接同一列中下一个非零元素。
• 十字链表存储需要额外的指针域、行、列指针
  • 一般的，当非零元的数不超过总元素个数的 20%，适用十字链表存储。