贪心算法
概述
贪心算法每步都采取当前最优(局部最优),最终得到一个全局最优的方案;
教室调度问题:
注:
- 上述中选择最早结束的课程的策略可以找到教室调度问题最优解;
- 选择最小占用时间的课程得不到最优解;
- 选择最早开始的课程得不到最优解;
- 贪心算法不是任何情况下都有效,但容易实现;
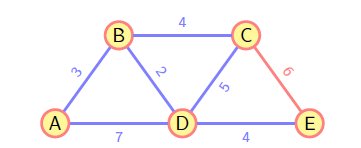
Prim
基本概念:生成树、最小生成树
算法核心:从连通
和 的边中挑选一条权重最小的边。
- 任意选一点
- 从连通
- 重复步骤 2,直到集合
python
def cmp(key1, key2):
return (key1, key2) if key1 < key2 else (key2, key1)
def prim(graph, init_node):
visited = {init_node}
candidate = set(graph.keys())
candidate.remove(init_node) # 添加所有除开始定点的其他顶点
tree = []
while len(candidate) > 0:
edge_dict = dict()
for node in visited: # 找到所有已访问的节点
for connected_node, weight in graph[node].items(): # 拿到与该节点相连的节点
if connected_node in candidate: # 没访问过就加入待选集
edge_dict[cmp(connected_node, node)] = weight
edge, cost = sorted(edge_dict.items(), key=lambda kv: kv[1])[0] # 从待选集找到最小的权重路径
tree.append(edge)
visited.add(edge[0]) # 把选中的加入已访问集合
visited.add(edge[1])
candidate.discard(edge[0]) # 把选中的移除已访问集合
candidate.discard(edge[1])
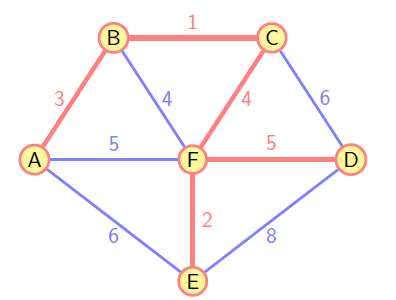
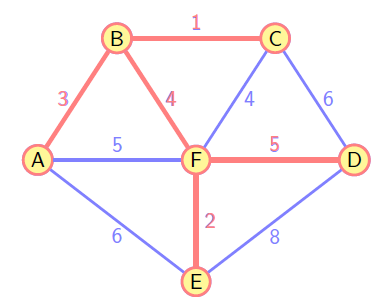
return treeKruskal
算法贪婪地选择最小权重的边,扩展无环的子图构造最小生成树。
- 按照权重非递减顺序对途中的边 E 进行排序;
- 烧苗已排序的列表,如果下一条边加入当前的子图中不导致一个回路,则加入该边到子图中,否则跳过该边;
- 重复步骤 2,直到子图中有
python
def cmp(key1, key2):
return (key1, key2) if key1 < key2 else (key2, key1)
def find_parent(record, node):
if record[node] != node:
record[node] = find_parent(record, record[node])
return record[node]
def naive_union(record, edge):
u, v = find_parent(record, edge[0]), find_parent(record, edge[1])
record[u] = v
def kruskal(graph):
edge_dict = {}
for node in graph.keys():
# cmp 把字母的顺序交换,update 去除相同的键从而去重
edge_dict.update({cmp(node, k): v for k, v in graph[node].items()})
# 按权重排序的边集合
sorted_edge = list(sorted(edge_dict.items(), key=lambda kv: kv[1]))
tree = []
connected_records = {key: key for key in graph.keys()}
for edge_pair, _ in sorted_edge:
if find_parent(connected_records, edge_pair[0]) != \
find_parent(connected_records, edge_pair[1]):
tree.append(edge_pair)
naive_union(connected_records, edge_pair)
return tree难点:判断新加入的边是否构成回路
并查集的思想
基本
- connected_records:生成一个单元素集合;
- find_parent(x):返回一个包含 x 的子集;
- union(x, y):构造分别包含 x 和 y 的不相交子集的并集;

要点
- 按照权重
- 判断
算法效率分析
- 第一步的时间复杂度为
- 第二步
- 快速查找:
- 快速求并:
- 快速查找下总的效率为
- 快速求并下总的效率为
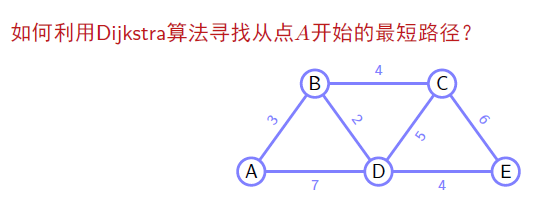
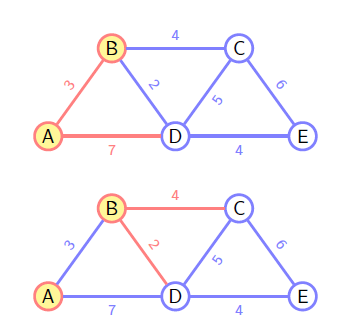
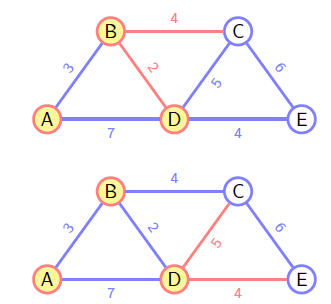
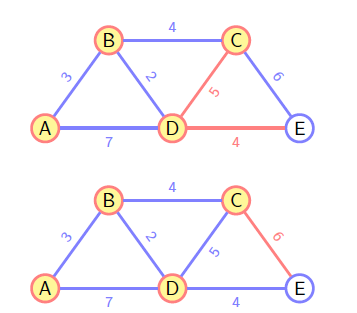
Dijkstra
和 Prim 类似,不过选择下一条路径时并不是判断的是当前权重,而是整条路径的权重作比较